La Seccion Aurea - Armonia del Universo
Es la ecuación escondida en la naturaleza y en objetos a todo nuestro alrededor, tan misteriosa como el secreto de su orígen - la Sección áurea (or Proporción Áurea) es un número irracional, una expresión matemática de perfecta armonía en el universo.
Más aún, la simplicidad de su construcción la hace aún más hermosa.
Toma una línea de cualquier largo (A) y divídela en dos secciones de diferente largo, a y b.
A= a + b
La división de su largo total (A) entre la sección más larga será igual a la división de sus dos secciones:
Aunque el filósofo y matemático griego Pitágoras tiene el crédito de haber estudiado la sección áruea ya en el siglo V antes de cristo, el orígen de esta ecuación matemática parece ser aún más antiguo y sus raíces se pierden en el tiempo.
De hecho, las proporciones de la Gran pirámide de Giza, construida alreadedor del 2560 A.C., se aproximan cercanamente a las de una pirámide áurea.
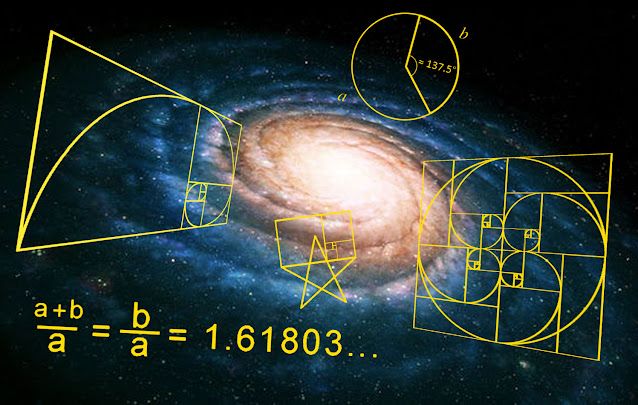
La sección áurea puede ser transferida a dos y tres dimensiones, dándonos así rectágulos áureos, espirales áureos, ángulos áureos y sólidos tridimensionales áureos.
Cuando es llevada a las dos dimensiones, el cálculo de arriba nos da un cuadrado y un rectángulo, los cuales juntos conforman un ‘Rectángulo áureo’.
Este rectángulo áureo contiene en sí infinitas repeticiones de sí mismo, siempre manteniendo la misma razón de 1,61803...
Cuando dibujamos curvas conectando las esquinas opuestas de cada cuadrado interno, obtenemos una ‘Espiral áurea’.
Cuando transferimos la proporción áurea a un círculo (la razón de 1,61803 expresada en rotaciones o grados), obtenemos el ‘Ángulo Áureo’.
Además, los antíguos griegos descubrieron la relación entre las proporciones de un pentáculo y la proporción áurea.
Esto llevó a los científicos griegos a creer que el dodecaedro (la versión tridimensional del pentáculo) era el sólido más perfecto en la naturaleza, la forma del universo mismo, y un misterio que no podía ser revelado a los no iniciados.
Afortunadamente, hoy sabemos más y mejor.
Los llamados números Fibonacci pueden darnos una aproximación al orígen de la proporción áurea.
Leonardo Bonacci (también conocido como Fibonacci) fué un matemático italiano del siglo XII que ayudó a popularizar el uso de los número indo-arábigos en Europa (en donde, hasta entonces, aún se trabajaba con numerales romanos).
Su exposición a la matemática indo-arábiga pueden haberle proporcionado la clave para su progresión matemática, más tarde llamada ‘números Fibonacci’. De acuerdo con varias fuentes calificadas, éstos números ya habrían estado presente en la antigua matemática india, así como en antiguas tablas babilónicas.
Los números Fibonacci son una simple progresión aritmética en la cual cada número es el resultado de la sumatoria de los dos numeros previos, empezando con el 0 y el 1. De ésta forma:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Tan simple como pueda parecer esta progresión, sus usos en matemática, estadística, cálculos de probabilidad, algoritmos computacionales y finanzas son infinitos y, aun más sorprendente, la razón de éstos numeros se aproxima mucho a los de la proporción áurea..
Mientras más elevado es el número Fibonacci, más cercana es su aproximación a la proporción áurea.
En el siglo XVI, el matemático alemán Simón Jacob ya encontró una relación entre los números Fibonacci y la proporción áurea, y ésto fue mas tarde confirmado por Johannes Kepler en 1608.
De hecho, si vemos la representación gráfica de los números Fibonacci, veremos que es muy parecida a un Rectángulo áureo.
Increíblemente, ésta progresión (y la de la proporción áurea) emerge de forma espontánea en muchas estructuras en la naturaleza, particularmente aquellas que deben comprimir grandes cantidades de elementos en un espacio limitado, o que requieren un crecimiento organizado sin molestar al resto de las partes ya existentes.
Por miles de años, gente de todas las culturas a través del mundo han utilizado este conocimiento matemático en diseño, arquitectura y las artes, ya que se cree que éstas proporciones crean los resultados más agradables y armoniosos en la pieza final.
Cuando dividimos el rectángulo áureo con dos líneas horizontales y verticales siguiendo sus proporciones internas, obtenemos cuatro ‘Punto Áureos’ dentro del rectángulo.
Estos puntos representan la sección favorecida naturalmente por nuestra atención dentro del área dada.
Esta estructura ha sido usada por artístas y fotógrafos por cientos de años para planificar y proporcionar sus obras de la manera más armónica y estética posible.
“Cristo en la Casa de sus Padres” - John Everett Millais
Además, muchos de los objetos cotidianos que nos rodean están diseñados basados en las proporciones de la sección áurea. He aquí algunos ejemplos:
¿Cuántos más puedes encontrar?
A diferencia de otros números irracionales, parte de la magia de la proporción áurea es que puede ser definida en términos de ella misma. Es decir, se contiene a sí misma infinitamente - tanto infinitamente grande como infinitamente pequeña.
Esto, a su vez, nos recuerda a una de las propiedades de otra fantástica construcción matemática: los fractales.
Se dice que las matemáticas son el lenguaje del universo, y la proporción áurea es el ejemplo perfecto de qué tan certera puede ser esta aseveración.
Bien invisible o justo frente a tus narices, las armoniosas proporciones de la sección áurea son tanto estéticas como prácticas, una fascinante combinación de arte y ciencia que continuará asombrándonos por muchas generaciones a futuro.
Artículos Relacionados
Los Fractales
Si disfrutaste este artículo, considera Compartirlo, o Subscríbete para recibir artículos similares una vez al mes en tu casilla de correo electrónico.
Fuentes: Wikipedia, MathIsFun.com, “La Sección Áurea: El Más Grande Secreto de la Naturaleza” por Scott Olsen (Bloomsbury).
Comments
Post a Comment